名词解析

1、逻辑结构和存储结构

• 逻辑结构：指的是数据元素之间的相互关系和组织方式，描述数据元素之间如何连接、关联。常见的逻辑结构有线性结构（如数组、链表）、树形结构（如二叉树）、图形结构等。
• 存储结构：指的是数据在计算机内存中具体的存储方式，是实现逻辑结构的具体方式。常见的存储 结构有顺序存储（如数组）、链式存储（如链表）等。

2、稳定的排序方法和不稳定的排序方法

• 稳定的排序方法：在排序过程中，相等的元素在排序后相对位置不变。例如，冒泡排序、插入排序、归并排序。
• 不稳定的排序方法：在排序过程中，相等的元素在排序后相对位置可能发生改变。例如，快速排序、选择排序、堆排序。

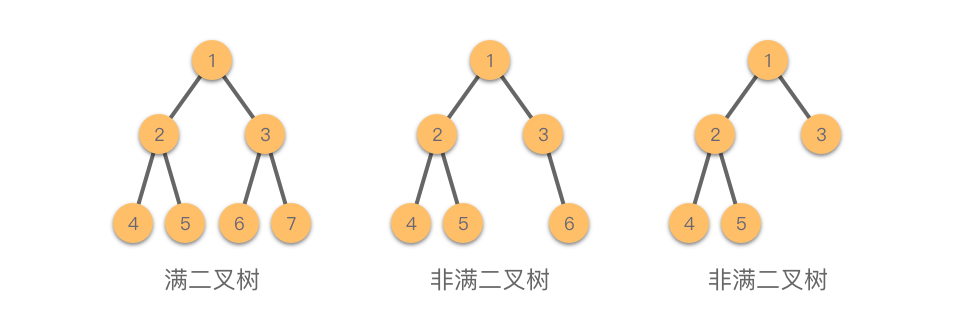
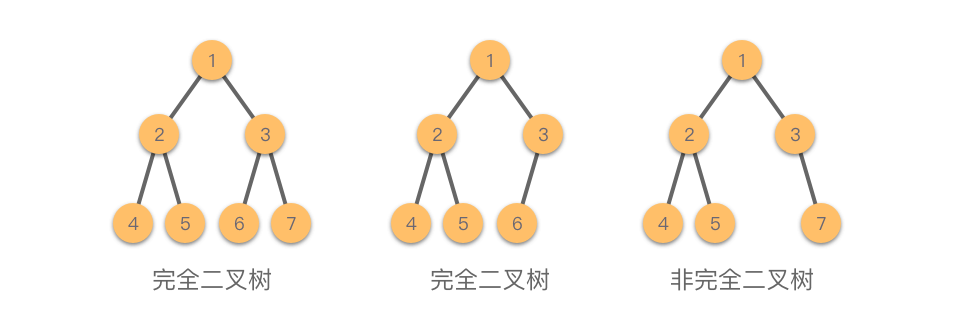
3.完全二叉树

• 完全二叉树：是一种特殊的二叉树，除了最底层外，其余每一层的节点数都达到最大，并且最底层的节点从左到右排列。完全二叉树的节点编号是按照从上到下、从左到右的顺序编号的。

4.什么是关键路径？什么是关键活动？

• 关键路径：在项目管理中，关键路径是指从项目开始到项目结束的所有任务所组成的路径，这条路径上的每个任务都不能延误，否则整个项目的完成时间将延长。关键路径上的活动即为关键活动。
• 关键活动：指在项目中，任何延误都将直接影响项目总工期的活动。它们位于关键路径上，是项目中最重要的活动。

5.什么是前缀编码？哈夫曼编码为什么是前缀编码？

• 前缀编码：是一种编码方式，任何一个编码都不是另一个编码的前缀。即没有任何一个编码是另一个编码的开头部分。常见的前缀编码有哈夫曼编码。
• 哈夫曼编码是前缀编码：因为在哈夫曼编码中，编码的构造保证了任何一个字符的编码都不可能是另一个字符编码的前缀，因此满足前缀编码的性质。哈夫曼编码通过使用变长的编码，使得频繁出现的字符用短的编码表示，而不常见的字符用长的编码表示，从而提高了编码效率。

6.什么是数据结构？常见的数据结构类型有哪些？

• 数据结构：是计算机中存储、组织数据的方式，它定义了数据元素之间的关系以及存取数据的方法。数据结构是实现算法的基础，它影响程序的执行效率和资源使用。
• 常见的数据结构类型:
  1. 线性数据结构：如数组、链表、栈、队列。
  2. 树形数据结构：如二叉树、AVL树、红黑树、B树、堆。
  3. 图形数据结构：如无向图、有向图、加权图、邻接矩阵、邻接表。
  4. 哈希表：通过哈希函数实现高效的查找和插入。
  5. 集合与映射：如集合、字典、集合运算等。

其他基础名词

1. 线性表：由若干数据元素构成的集合，其中的元素之间存在一对一的关系。常见的线性表有数组、链表、栈、队列等。
2. 栈：一种线性数据结构，遵循后进先出（LIFO）原则，只有一个端口可以插入和删除元素。
3. 队列：一种线性数据结构，遵循先进先出（FIFO）原则，元素从队尾插入，从队头删除。
4. 数组：一种线性数据结构，通过连续的内存单元存储相同类型的数据元素，可以通过索引进行访问。
5. 链表：一种线性数据结构，元素通过指针连接，每个元素包含数据和指向下一个元素的指针。
6. 双向链表：一种链表结构，除了每个元素指向下一个元素的指针外，还包含指向前一个元素的指针。
7. 树：由若干个节点组成的非线性数据结构，节点之间有父子关系。
8. 二叉树：每个节点最多有两个子节点的树。
9. 二叉搜索树：一种特殊的二叉树，左子树的值小于根节点的值，右子树的值大于根节点的值。
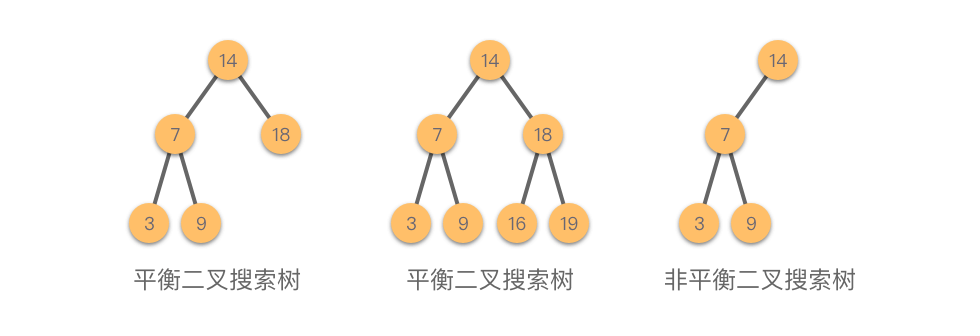
10. 平衡二叉树：一种特殊的二叉树，**任何节点的左右子树的高度差不超过1。**时间复杂度为 O(log n)
11. 哈希表：通过哈希函数将键值映射到一个位置，常用于实现高效的查找、插入操作。
12. 图：由顶点和边组成的数据结构，边表示顶点之间的关系。一般用数字表示。
13. 邻接矩阵：一种表示图的方式，使用二维数组表示顶点之间的连接关系。
14. 邻接表：另一种表示图的方式，使用链表或动态数组表示每个顶点的邻接节点。
15. 深度优先搜索（DFS）：一种图的遍历方法，优先访问深层节点，直到没有未访问的邻接节点时返回。
16. 广度优先搜索（BFS）：一种图的遍历方法，优先访问浅层节点，逐层遍历图的节点。
17. 递归：一种函数调用自身的编程方式，通常用于解决可以分解为更小规模相同问题的任务。
18. 动态数组：一种数组类型，具有可变大小的特性，支持动态扩展
19. 堆：一种完全二叉树结构，用于实现优先队列。最大堆或最小堆根据优先级决定元素的排列。
20. 动态规划：一种将复杂问题分解成小问题，解决小问题并存储其解，最后合成大问题解的算法设计方法。
21. 迭代：通过循环结构逐步逼近目标结果的方法，适用于不需要递归的场景。
22. 并查集：一种用于处理不相交集合合并和查询的问题的数据结构。支持两种操作：查找（判断两个元素是否属于同一集合）和 合并（将两个集合合并成一个）。
    • 路径压缩：优化查找操作，减少树的高度。
    • 按秩合并：优化合并操作，避免形成过高的树
23. 哈希冲突：当两个不同的键值通过哈希函数映射到相同的位置时，称为哈希冲突。常见的解决方法有链式法和开放地址法。
    • 链式法：使用链表来解决冲突，多个元素可以存储在同一个位置。
    • 开放地址法：当发生冲突时，寻找下一个空闲位置进行插入。
24. 红黑树：一种自平衡的二叉搜索树，具有更多的约束条件，能够保证最坏情况下的 O(log n) 查找、插入和删除操作。
25. 时间复杂度：衡量算法执行时间随输入规模变化的增长率。常用的时间复杂度有 O(1)、O(log n)、O(n)、O(n log n)、O(n²) 等。
26. 空间复杂度：衡量算法所需空间随输入规模变化的增长率
27. 最小生成树
    • Prim算法：从一个点开始逐步加入最小的边，直到包含所有点。
    • Kruskal算法：从最小的边开始逐步加入，不形成环，直到生成树完整。
28. 常见排序算法：
    • 冒泡排序：O(n^2)
    • 选择排序：O(n^2)
    • 插入排序：O(n^2)
    • 归并排序：O(n log n)
    • 快速排序：O(n log n)（平均）
    • 堆排序：O(n log n)
29. 图的存储方式
    • 邻接矩阵：适用于稠密图。
    • 邻接表：适用于稀疏图。
30. 线索二叉树是对二叉树的一个改进，用来避免在遍历时使用栈或递归，使用线索指针替代空指针。

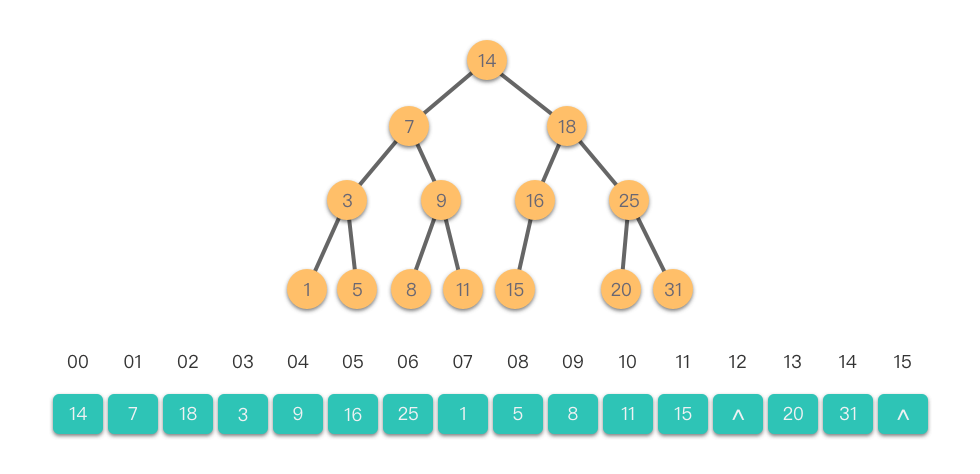
图片展示

简答

队列计算

队列的长度

1

length=(r-f+m)%m

队满的条件

1

(r+1)%m == f

队列不满的时候入队

1

r=(r+1)%m

队空的条件

1

f == r

队列不为空时出队

1

f = (f+1)%m

• r 是队尾指针
• f 是队头指针
• m 是队列的最大容量

广义表计算

广义表的表长是指广义表中直接包含的元素个数，而这些元素可以是原子（如 a、b）或者子表。注意是直接包含

例：

1

LS = (a, b, c), (d, e, f)

上面LS的表长即为2

广义表的提取：

下面

1

head(tail(tail(head(LS))))

即结果为元素c

就是先分析里面的，然后一层一层的套，最后只剩下一个了得head取出

例如：

取出元素e

1

head(tail(head(tail(LS)))) = e

树的计算

对于完全二叉树来说，n为总节点树，[x]为向上取整

叶子节点的数量L

1

L=[n/2]

对于完全二叉树，除了最后一层外，其他层的结点都是满的，所以大部分叶子结点都在最后一层或倒数第二层。

树的深度：

是指从根结点到最深叶子结点的路径长度，对于完全二叉树则深度d为

1

d=⌈log2(n)⌉

完全二叉树的深度为 d，则结点数 n 满足：
$$
2^{d-1} \leq n \leq 2^d - 1
$$

• 一个完全二叉树的最小结点数发生在只有根节点的情况下，深度为 dd 的完全二叉树的最小结点数是 2d−12d−1。
• 完全二叉树的最大结点数是满二叉树的结点数，即 2d−12d−1。

非叶子结点的个数可以通过以下公式计算：

$$
N_{non-leaf} = n - L
$$

图的计算

完全图的边和顶点的关系，假设m条边和n个顶点，图的边数为
$$
m= n(n−1)/2
$$
非连通无向图考虑至少顶点数的情况下，该图由两个子图构成，一个是完全图一个是只有一个顶点，所以如果边数为28的话，最后至少9个顶点。

那我们接下来来考虑至多的情况

对于非连通无向图，最多顶点数的情况是图中每个连通分量都为一个孤立的顶点，即每个顶点都没有边。但是题目限定了28条边，那我们就每个连通分量都拥有尽可能少的边数，也就是两个顶点一条边。边数为28的话，那么顶点数就是56。所以至多顶点数为56

时间复杂度分析

1
2
3
4
5

x = 0;
for(i = l; i < n; i++)
  for(j = l; j <= n - i; j++)
    x++;

时间复杂度为O(n^2)

1
2
3
4
5

i = -l;
for(j = l; j <= n; j++)
  while(i <= n)
    i = i * 2;

时间复杂度为*O(n log n)

在简单for循环中时间复杂度可以为

1

外层时间复杂度*内层时间复杂度

数组计算

1、设有一个二维数组 A[m][n]按行优先顺序存储，假设 A[0][0]存放位置在
644(10)，A[2][2]存放位置在 676(10)，每个元素占一个字节的空间，问 A[3]3
存放在什么位置？脚注(10)表示用 10 进制表示。

元素 A[i][j]A[i][j] 的存储地址可以通过以下公式计算：
$$
地址(A[i][j])=地址(A[0][0])+(i×n+j)
$$

• i 是行号，
• j 是列号，
• n 是数组的列数，
• 地址(A[0][0])地址(A[0][0]) 是数组的起始位置。

这样解出n=15然后获得a33的位置

查找算法

折半查找

在折半查找中，判定树是根据每次比较将序列分为两部分来进行的

假设我们有一个长度为 12 的序列，元素的下标从 1 到 12。

• 初始查找范围：整个序列，长度为 12，范围是从 1 到 12。

• 选择中间的元素。中间元素的下标是 (1 + 12) / 2 = 6，所以在第一次比较时，根结点的值是序列中的第 6 个元素。

• 如果要找的值比根结点的值小，查找范围变为 1 到 5。

• 如果要找的值比根结点的值大，查找范围变为 7 到 12。

• 如果查找范围是 7 到 12，那么新的中间元素下标为 (7 + 12) / 2 = 9。此时，根结点的右孩子的值对应的是序列中的第 9 个元素。

在折半查找中，若得到的中间元素位置是小数，则需要向下取整。

孩子节点就是子节点

真题练习

哈夫曼树的构建

已知下列字符 A、B、C、D、E、F、G 的权值分别为 3、12、7、4、
2、8，11，试填写出其对应哈夫曼树 HT 的存储结构的终态，完成表 1。
表 1 哈夫曼树 HT 的存储结构的终态
weight parent lchild rchild
1
2
3
4
5
6
7

因为哈夫曼树是从最小的节点一次累加最后聚合到根节点

所以把上面权按照大小顺序排列

【2,3,4,7,8,11,12】

然后按照大小顺序合并

第一次：[4,5,7,8,11,12]

第二次：[7,8,9,11,12]

第三次：[9,11,12,15]

第四次：[12,15,20]

第五次：[20,27]

第六次：[47]

所以最后的根节点就是47

所以最后得到的哈夫曼树就是

1
2
3
4
5
6
7
8
9
10

                  (47)
                /     \
             (20)     (27)
            /   \     /     \
       (9)     (11) (12)   (15)
      /  \     		      /   \
   (4)    (5) 			(7)   (8) 
  		 /  \
（2） (3)  

哈夫曼编码就是从根节点开始，往左走是0，往右走是1

所以权值为2的节点可以表示为0010,3可以表示为0011

然后分别按照出现的先后顺序填写好编号，再把节点的表填完

图-网

2、如下图所示的 AOE-网：
（1） 求这个工程最早可能在什么时间结束；
（2） 求每个活动的最早开始时间和最迟开始时间；
（3） 确定哪些活动是关键活动。

这个主要就是带权图的知识

设使用每个步骤所用的最早可能开始时间为e，所用的最迟可能开始时间为l

当l-e=0的时候为关键活动。

查找长度

设哈希函数 H（K）=3 K mod 11，哈希地址空间为 0～10，对关键字
序列（32，13，49，24，38，21，4，12），按链地址法（拉链法）构造哈希表，并
分别求出等概率下查找成功时和查找失败时的平均查找长度 ASLsucc 和
ASLunsucc。

其中mod11是指取余的意思

那么根据运算公式h(k)=3kmod11

h(32)=32*3mod11=8

h(13)=13*3mod11=6

h(49)=48*3mod11=4

h(24)=24*3mod11=6

h(38)=38*3mod11=3

h(21)=21*3mod11=8

h(4)=4*3mod11=1

h(12)=12*3mod11=3

所以链表的构造为

位置 data length

0 null

1 4 1

2 null

3 38->12 2

4 49 1

5 null

6 13->24 2

7 null

8 32->21 2

9 null

10 null

查找成功时的平均查找长度是所有成功查找的查找长度的平均值。每个位置的查找长度等于该位置链表的长度。假设每个位置的链表长度为 L(i)，则查找成功的平均查找长度为：
$$
ASLsucc=
成功查找次数
∑L(i)/成功查找次数
$$
所以Aslsucc=8/8=1

查找失败时的平均查找长度是所有失败查找的查找长度的平均值。查找失败时的查找长度是从位置 0 到位置 10 的每个位置的查找深度（即链表长度）。如果某个位置没有元素（空），则查找长度为 1。

Aslunsucc=13/10=1.3

设一组有序的记录关键字序列为(13，18，24，35，47，50，62，83，90)，查找方法用二分查找，要求计算出查找关键字62时的比较次数并计算出查找成功时的平均查找长度。

索引是从[0-8]所以中间元素是47，47<62所以范围是[5-8]

中间元素正好是62

所以比较次数为2
$$
ASL=

1×C
1
​
+2×C
2
​
+⋯+n×C
n/n
$$
最坏情况下，需要 log⁡2n\log_2 nlog2n 次比较（如果是成功查找）。对于这个数组，n=9n = 9n=9，所以最多需要 log⁡2 9≈3.17次比较，四舍五入就是 4 次比较。

对于数组长度 n=9n = 9n=9，各个元素成功查找时的比较次数：这个是需要四舍五入的

1个是1次，两个三个是2次，四个五个六个是3次，七个八个九个是4次
$$
ASL=

（1+4+2+9+6+6+8+4+8）/9

9/
48
​
≈2.67
$$

二叉树的遍历和森林转换

设一棵二叉树的先序序列： A B D F C E G H ，中序序列： B F D A
G E H C

先序遍历的顺序是 根->左->右；中序遍历的顺序是 左->根->右

后序遍历是左->右->根

根据先序遍历获得根节点A

已知先序遍历和后序遍历是不能唯一确定一颗二叉树的，但是其他序列的组合是可以的。也就是确定唯一的二叉树必须要有中序遍历

根据中序遍历，D在B的右边，所以D是B的右子树。同样的E在C的左边，所以E是C的左子树

所以还原出来的二叉树是

1
2
3
4
5
6
7
8

   A
 /   \
B    	 C
 \     /
  D  	 E
 /   	/ \
 F  	G   H

然后他的后序遍历是

FDBGHECA

在这部分，我们要将二叉树转换为树或森林。要构建森林，我们将树的结构分为多个独立的子树。

分成两棵树

只要看这棵二叉树的根结点有没有右孩子，有的话就是森林，没有的话就是一棵树

第一步，若结点 x 是其双亲 y 的左孩子，则把 x 的右孩子，右孩子的右孩子等等等等，依次都与 y 用连连连接起来。

第二部，去掉所有双亲到右孩子之间到连线

然后从森林变成树的话就是这个操作的逆向

就是先把去掉右孩子的连线

然后把一棵树上相同深度的节点连起来

再把根节点连在一起

整理一下就得到了二叉树

设一棵树T中边的集合为{(A，B)，(A，C)，(A，D)，(B，E)，(C，F)，(C，G))，要求用孩子兄弟表示法（二叉链表）表示出该树的存储结构并将该树转化成对应的二叉树。

根据上面的信息，树应该是这样的

1
2
3
4
5
6

     A
   / | \
  B  C  D
 /   / \
E   F   G

设有一组初始记录关键字为(45，80，48，40，22，78)，要求构造一棵二又排序树并给出构造过程

根据插入顺序插入元素，大于根节点的为右子树，小于的则为左子树

对于每个节点，左子树的所有节点值都小于该节点值，右子树的所有节点值都大于该节点值。通过这种方式保证了树的结构满足二叉排序树的特性。所以二叉搜索树如下

1
2
3
4
5
6

     45
    /  \
  40    80
 /     /  \
22    48  78

排序

设待排序的关键字序列为{12，6，16，30，10，20，2，18}，试分别写
出使用以下排序方法第一趟排序结束后关键字序列的状态，并写出该算法是稳定的
还是不稳定的。
① 希尔排序（d1=3）
② 冒泡排序
③ 快速排序
④ 二路归并排序

⑤选择排序

希尔排序：

希尔排序的基本思路是：先将待排序序列按一定增量分组，分别对每组元素进行插入排序，最后逐步缩小增量，直到增量为 1，再进行一次插入排序。

给定增量序列：d1=3d_1 = 3d1=3，所以分组的方式是每隔 3 个元素一组。

首先，将序列按增量 3 分成 3 组：

• 组 1：{12, 30, 2}
• 组 2：{6, 10, 18}
• 组 3：{16, 20}

对每组分别进行插入排序：

• 组 1：{12, 30, 2} -> 排序后为 {2, 12, 30}
• 组 2：{6, 10, 18} -> 排序后为 {6, 10, 18}
• 组 3：{16, 20} -> 排序后为 {16, 20}

然后重新合并这些组，得到：

{2,6,16,12,10,20,30,18}

在这之中，插入排序是稳定的。因为在排序过程中，当遇到相同的元素时，它们的相对顺序不会改变。最坏的结果下，时间复杂度是o(n^2)

希尔排序通常被认为是不稳定的，因为它在分组排序过程中可能会改变元素的相对顺序，特别是在增量较大时。

冒泡排序：

{12，6，16，30，10，20，2，18}

直接进行相互比较，后边的小就往前移动，大就不移动

然后经过第一趟之后是：

{6，12，16，10，20，2，18，30}

冒泡排序是稳定的。即使相同的元素出现，也会保留它们原来的相对顺序。

快速排序：

快速排序的基本思路是：选择一个基准元素，将数组分成两个部分，左边部分小于基准，右边部分大于基准，再递归排序两个部分。

{12，6，16，30，10，20，2，18}

以12为基准，小于12的{6,10,2}

大于12的{16,30,20,18}

然后合并，把基准12放在合适的位置，得到

{6,10,2,12,16,30,20,18}

快速排序是非稳定的，因为相同的元素在分区过程中可能会改变原有的相对位置。

二路归并排序:

二路归并排序的基本思路是：将序列不断分成两部分，递归地对两部分排序，最后合并排序好的两部分。

如何根据长度n划分部分

如果 n 是偶数，两个子序列的长度相等。

如果 n 是奇数，前一个子序列的长度是 n // 2，后一个子序列的长度是 n // 2 + 1。

{12，6，16，30，10，20，2，18}

分成两部分，然后每部分进行排序

{12，6，16，30}->{6,12,16,30}

{10，20，2，18}->{2,10,18,20}

然后合并两部分

{6,12,16,30,2,10,18,20}

归并排序是稳定的。在合并过程中，如果两个元素相等，它们的顺序会保留。

选择排序

简单 选择排序通过每一趟选择剩余序列中的最小值并将其放到已排序部分的末尾。

{12，6，16，30，10，20，2，18}

第一次找到最小值2与12交换，得到

{2,6,16,30,10,20,12,18}

稳定性：不稳定。因为最小元素可能会被交换，从而改变相等元素的相对顺序。

然后还有直接插入排序

从第二个元素开始，与前面的已排序部分逐一比较，找到合适的位置插入当前元素。

最小堆和最大堆

最小堆（即根节点是最小值）。最小堆是一个完全二叉树，它满足每个父节点的值都不大于其子节点的值。每次向堆中插入数据时，都需要通过"上浮"（bubble-up）操作来维持堆的性质。

画出向小根堆中加入数据4，2，5，8，3时，每加入一个数据后堆的变化。

首先加入4，4是根节点

然后加入2，2小于4,所以交换2和4，2为根节点

1
2
3
4

  2
 /
4

然后加入5，因为5比2大，所以不用上浮

1
2
3
4

  2
 / \
4   5

然后加入8，8大于2，不需要上浮

1
2
3
4
5

    2
   / \
  4   5
 /
8

插入3，3小于4交换3和4，然后3大于2，不需要再上浮

1
2
3
4
5
6

    2
   / \
  3   5
 / \
8   4

所以这就是最终的堆

1
2
3
4
5
6

    2
   / \
  3   5
 / \
8   4

然后大根堆的话就是根节点是最大的值，其他的操作和最小堆一样

比如加入2, 3, 5, 8, 4

先加入2，作为根节点

然后加入3，3比2大，然后23交换

1
2
3
4

  3
 /
2

加入5，5比2大，25交换，5比3大，53交换

1
2
3
4

  5
 / \
2   3

加入8，8大于5，85交换，8大于3交换83

1
2
3
4
5
6

    8
   / \
  5   3
 /  
2

最后插入4

1
2
3
4
5
6

    8
   / \
  5   3
 / \  
2   4

大根堆和堆排序

堆排序是一种选择排序

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

左子节点就是2i+1,右子节点就是2i+2

父节点在(i-1)/2

将序列（5，26，77，1，61，11）构造成大根堆并实现排序，请画出
初始形态和最终的大根堆，并写出第一趟堆排序的结果。

在这里构造大根堆的时候，根节点要最大

从最后一个非叶子节点开始（也就是数组中的 n//2 - 1 位置），依次向前执行"堆化"操作，确保每个子树都满足大根堆的性质。

堆化节点1 index=2

左子节点：77，右子节点：11。最大值是 77。左子节点是2i+1 右子节点是2i+2

交换 77 和 5，得到 [77, 26, 5, 1, 61, 11]。

然后堆化节点0 index=1

左子节点是26 右子节点是61

交换26和61

[77，61，5，1，26，11]

堆化节点0 index=0

77是最大不用堆化

所以大根堆是

1
2
3
4
5
6

    77
   /  \
  61   5
 /  \   \
1   26  11

堆排序的方法：

将堆顶（最大元素）与堆的最后一个元素交换。

调整堆，重新保证堆的性质。

重复步骤 1 和 2，直到堆的大小为 1。

实例：

最后肯定是堆化排序成[1, 5, 11, 26, 61, 77]

第一步是交换77和11

所以其顺序变成了

[11，61，5，1，26，77]

迪杰拉斯特算法和prim算法

迪杰斯特拉（Dijkstra）算法是一种用于解决单源最短路径问题的算法，尤其适用于图的边权重为非负数的情况。它的目标是找到从一个起点（源节点）到图中所有其他节点的最短路径。

初始化：给定图的每个节点，设定起点的最短路径为0，其余节点的最短路径为无穷大。

选择当前节点：在尚未确定最短路径的节点中，选择一个具有最短路径估计值的节点。

更新邻居节点的最短路径：对当前节点的每个邻居节点，通过比较现有的最短路径和通过当前节点到该邻居的路径来更新邻居节点的最短路径。

标记当前节点为已处理：一旦确定了当前节点的最短路径，就将其标记为“已处理”。

重复：重复步骤2至步骤4，直到所有节点的最短路径都被确定。

就是找最小的路径，然后访问所有的节点，注意是无向图还是有向图

在表格中，没有办法直接到达的写无穷，然后能直接俄到达的直接写，然后写出路径，权值。已经到达的不写用\

prim算法就是找到最小生成树，方法是通过起点，然后依次出发找到下一个点，使其经过的路程的和最小，只要是经过的点，都可以在那里出发去没有经过的点。

DFS和BFS遍历树

比如上面的邻接矩阵，0代表图没用相连，1代表相连了。

然后实现 深度优先搜索（DFS）

首先是深度，尽可能的往下扎

实现广度优先搜索（BFS）

线性表的计算（邻接矩阵和邻接表）

如图下列数组中存储了一个线性表，表头指针是A[0].next那么这个线性表是

就是看next指针，然后按顺序读取数据就行

{40,50,10,30,60,20}

然后画邻接矩阵和邻接表的时候

邻接矩阵就是图中1和5有连接，那么(1,5)和(5,1)的话就是1，如果是单向的箭头注意分清方向

然后邻接图的话类似用箭头和方块表示，最后没了的话就在后面的next画上**^**

算法设计

折半查找

试写出折半查找的递归算法。
//r 是有序表，查找关键字 k，若查找成功，返回 k 所在位置，查找失败返回 0。
int BinSearch（int r[ ]，int k，low，high）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

#include    <stdio.h>
int BinSearch(int r[],int k,int low,int high){
    if(low>high){
        return 0;
        
    }
    int mid = (low+high)/2;
    if(r[mid]==k){
        return mid+1;
    }
    else if(r[mid]>k){
        return BinSearch(r,k,low,mid-1);
    }
    else{
        return BinSearch(r,k,mid+1,high);
    }
}

写出折半查找的非递归算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14

int BinSearchNotFor(int r[],int k ,int low ,int high){
    while(low<=high){
        int mid = (low+high)/2;
        if(r[mid]==k){
            return mid+1;
        }
        else if(r[mid]>k){
            high = mid-1;
        }
        else{
            low =mid+1;
        }
    }
}

单链表查找

设计算法：统计单链表 HL 中结点的值等于给定值 x 的结点数。
int CountX(LNode* HL,ElemType x)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

typedef int ElemType;
typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode;
int CountX(LNode* HL,ElemType x){
    int count = 0;
    LNode* current = HL;
    while (current!=NULL)
    {
        if(current->data == x){
            count++;
        }
        current = current->next;
    }
    return count;
}
    

单链表查找最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define MM -1000
typedef int ElemType;
typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode,*LinkList;
ElemType Max(LinkList L){
    if(L==NULL||L->next ==NULL){
        return MM;
    }
    ElemType maxval = MM;
    LNode* current = L->next;
    while(current!=NULL){
        if(current->data>maxval){
            maxval = current->data;
        }
        current = current->next;
    }
    return maxval;
}

链表中节点的插入：

设指针变量p指向双向链表中结点A，指针变量g指向被插入结点B，要求给出在结点A的后面插入结点B的操作序列（设双向链表中结点的两个指针域分别为llink和 rlink)。

插入一个节点的时候，首先两个节点连接起来，然后把两个节点的前驱和后继再连接起来

1
2
3
4
5
6

A->rlink = B;
B->llink = A;
B->rlink = A->rlink;
if(A->rlink !=null){
A->rlink->llink = B;
}

快速排序实现

设有一组初始记录关键字序列（K1，K2，，Kn），要求设计一个算法能够　在○(n)的时间复杂度内将线性表划分成两部分，其中左半部分的每个关键字均小于 Ki，右半部分的每个关键字均大于等于Ki。

快速排序的基本思路是：选择一个基准元素，将数组分成两个部分，左边部分小于基准，右边部分大于基准，再递归排序两个部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include <stdio.h>

int partition(int arr[],int n,int pivoIndex){
    int pivot = arr[pivoIndex];
    int left = 0;
    int right = n-1;


    int temp = arr[pivoIndex];
    arr[pivoIndex] = arr[right];
    arr[right] = temp;

    while(left<right){
        while(left<right && arr[left]<pivot){
            left++;
        }
        while(left<right && arr[right]>=pivot){
            right--;
        }
        if(left<right){
            temp = arr[left];
            arr[left] = arr[right];
            arr[right] = temp;
        }
    }
    arr[n-1] = arr[left];
    arr[left] = pivot;
    return left;
}

求交集，设有两个集合A和集合B，要求设计生成集合C=AnB的算法，其中集合A 、B和C用链式存储结构表示。 （分析采用何种数据结构表示集合

使用链表来解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

#include <stdio.h>
#include <stdlib.h>

typedef struct Node{
    int data;
    struct Node* next;

}Node;

Node* createNode(int data){
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

void insertNode(Node** head,int data){
    if(*head == NULL){
        *head = createNode(data);
    }else{
        Node* temp = *head;
        while(temp->next != NULL){
            temp = temp->next;
        }
        temp->next = createNode(data);
    }
}
int existINList(Node* head,int data){
    Node* temp = head;
    while(temp != NULL){
        if(temp->data == data){
            return 1;
        }
        temp = temp->next;
    }
    return 0;
}
Node* andList(Node* A,Node* B){
    Node* C = NULL;
    Node* temp = A;
    while(temp != NULL){
        if(existINList(B,temp->data)){
            insertNode(&C,temp->data);
        }
        temp = temp->next;
    }
    return C;
}